Loading... # Manacher's Algorithm 马拉车算法 > 马拉车算法 Manacher‘s Algorithm 是用来查找一个字符串的最长回文子串的线性方法,由一个叫Manacher的人在1975年发明的,这个方法的最大贡献是在于将时间复杂度提升到了线性。 首先我们解决下奇数和偶数的问题,在每个字符间插入"#",并且为了使得扩展的过程中,到边界后自动结束,在两端分别插入 "^" 和 "\$",两个不可能在字符串中出现的字符,这样中心扩展的时候,判断两端字符是否相等的时候,如果到了边界就一定会不相等,从而出了循环。经过处理,字符串的长度永远都是奇数了。 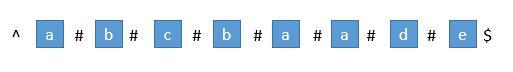 首先我们用一个数组 P 保存从中心扩展的最大个数,而它刚好也是去掉 "#" 的原字符串的总长度。例如下图中下标是 6 的地方。可以看到 P[ 6 ] 等于 5,所以它是从左边扩展 5 个字符,相应的右边也是扩展 5 个字符,也就是 "#c#b#c#b#c#"。而去掉 # 恢复到原来的字符串,变成 "cbcbc",它的长度刚好也就是 5。  ## 求原字符串下标 用 P 的下标 i 减去 P [ i ],再除以 2 ,就是原字符串的开头下标了。 例如我们找到 P[ i ] 的最大值为 5 ,也就是回文串的最大长度是 5 ,对应的下标是 6 ,所以原字符串的开头下标是 (6 - 5 )/ 2 = 0 。所以我们只需要返回原字符串的第 0 到 第 (5 - 1)位就可以了。 ## 求每个 P [ i ] 接下来是算法的关键了,它充分利用了回文串的对称性。 我们用 C 表示回文串的中心,用 R 表示回文串的右边半径。所以 R = C + P[ i ] 。C 和 R 所对应的回文串是当前循环中 R 最靠右的回文串。 让我们考虑求 P [ i ] 的时候,如下图。 用 i\_mirror 表示当前需要求的第 i 个字符关于 C 对应的下标。 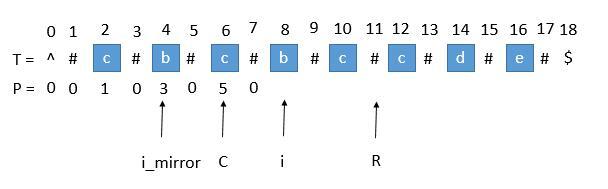 我们现在要求 P [ i ], 如果是用中心扩展法,那就向两边扩展比对就行了。但是我们其实可以利用回文串 C 的对称性。i 关于 C 的对称点是 i\_mirror ,P [ i\_mirror ] = 3,所以 P [ i ] 也等于 3 。 但是有三种情况将会造成直接赋值为 P [ i\_mirror ] 是不正确的,下边一一讨论。 ### 1. 超出了 R 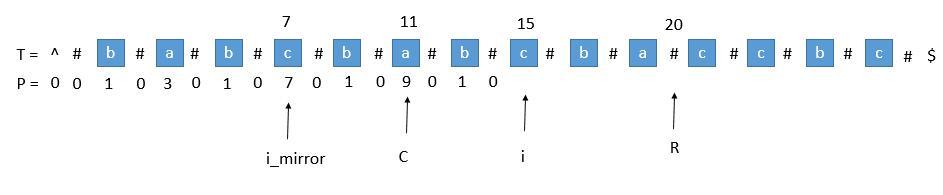 当我们要求 P [ i ] 的时候,P [ mirror ] = 7,而此时 P [ i ] 并不等于 7 ,为什么呢,因为我们从 i 开始往后数 7 个,等于 22 ,已经超过了最右的 R ,此时不能利用对称性了,但我们一定可以扩展到 R 的,所以 P [ i ] 至少等于 R - i = 20 - 15 = 5,会不会更大呢,我们只需要比较 T [ R+1 ] 和 T [ R+1 ]关于 i 的对称点就行了,就像中心扩展法一样一个个扩展。 ### 2. P [ i\_mirror ] 遇到了原字符串的左边界 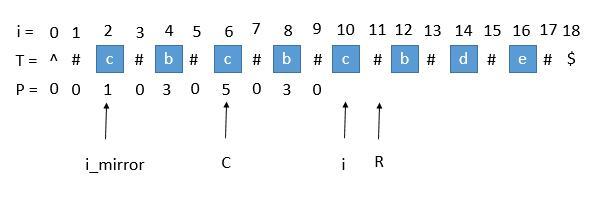 此时P [ i\_mirror ] = 1,但是 P [ i ] 赋值成 1 是不正确的,出现这种情况的原因是 P [ i\_mirror ] 在扩展的时候首先是 "#" == "#" ,之后遇到了 "^"和另一个字符比较,也就是到了边界,才终止循环的。而 P [ i ] 并没有遇到边界,所以我们可以继续通过中心扩展法一步一步向两边扩展就行了。 ### 3. i 等于了 R 此时我们先把 P [ i ] 赋值为 0 ,然后通过中心扩展法一步一步扩展就行了。 ## 考虑 C 和 R 的更新 就这样一步一步的求出每个 P [ i ],当求出的 P [ i ] 的右边界大于当前的 R 时,我们就需要更新 C 和 R 为当前的回文串了。因为我们必须保证 i 在 R 里面,所以一旦有更右边的 R 就要更新 R。 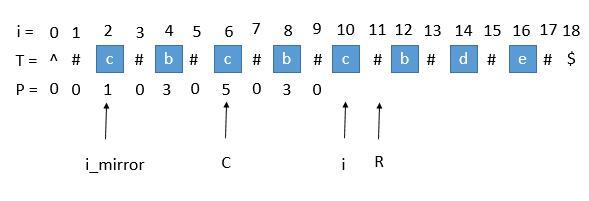 此时的 P [ i ] 求出来将会是 3 ,P [ i ] 对应的右边界将是 10 + 3 = 13,所以大于当前的 R ,我们需要把 C 更新成 i 的值,也就是 10 ,R 更新成 13。继续下边的循环。 **自实现** ```java /** * Manacher */ public int countSubstrings(String s) { int len = s.length(); StringBuilder sb = new StringBuilder("$#"); // 解决回文串奇数长度和偶数长度的问题,处理方式是在所有的相邻字符中间插入 '#' ,这样可以保证所有找到的回文串都是奇数长度的 for (int i = 0; i < len; ++i) { sb.append(s.charAt(i)).append('#'); } // 设置哨兵,到了边界就一定会不相等,从而结束循环 sb.append('%'); len = sb.length(); // 用 radius[i] 来表示以 sb 的第 i 位为回文中心,可以拓展出的最大回文半径 int[] radius = new int[len]; // 维护 当前最靠右的回文右端点 maxRight , 以及这个回文右端点对应的回文中心 maxMid int maxMid = 0; int maxRight = 0; int rs = 0; // 剪枝 for (int currMid = 2; currMid < len - 2; currMid++) { // radius[currMid] = [maxRight - currMid, radius[currMid 关于 maxMid 对称点]] // currMid 在当前最大回文子串内: // 回文串的性质,关于回文中心对称的两边一样,因此当前点的回文半径至少是对称点的回文半径 // 因此 currMid 处的 回文半径 最小为 对称点的最大回文半径 // 特殊情况:currMid + 对称点的最大回文半径 > maxRight // 此时无法取到整个对称点的最大回文半径 , 但最小可以是 currMid 到 maxRight 之间 // currMid 不在当前最靠右的回文串内: // 以 currMid 为中心 1 为回文半径 radius[currMid] = currMid <= maxRight ? Math.min(maxRight - currMid + 1, radius[2 * maxMid - currMid]) : 1; // 中心拓展 while (sb.charAt(currMid + radius[currMid]) == sb.charAt(currMid - radius[currMid])) { radius[currMid]++; } // 动态维护 maxMid 和 maxRight // 当前回文右端点 = 当前中心 + 最大回文半径 - 1 > 最大回文右端点 if (currMid + radius[currMid] - 1 > maxRight) { maxMid = currMid; maxRight = currMid + radius[currMid] - 1; } // 最长回文子串的结尾一定是 '#' , 因为如果结尾是有实际意义的字符,其两端一定都是 '#' // 中心位置如果是 '#' 则半径为偶数 // # a # b [#] b # a # 此时回文半径为 4 , 4 >> 1 == 2 // 如果为实际意义的字符则半径为奇数向下取整 // # a # b # [currMid] # b # a # 此时回文半径为 5 , 5 >> 1 == 2 rs += radius[currMid] >> 1; } return rs; } ``` **通用实现** ```java public String preProcess(String s) { int n = s.length(); if (n == 0) { return "^$"; } String ret = "^"; for (int i = 0; i < n; i++) ret += "#" + s.charAt(i); ret += "#$"; return ret; } // 马拉车算法 public String longestPalindrome2(String s) { String T = preProcess(s); int n = T.length(); int[] P = new int[n]; int C = 0, R = 0; for (int i = 1; i < n - 1; i++) { int i_mirror = 2 * C - i; if (R > i) { P[i] = Math.min(R - i, P[i_mirror]);// 防止超出 R } else { P[i] = 0;// 等于 R 的情况 } // 碰到之前讲的三种情况时候,需要利用中心扩展法 while (T.charAt(i + 1 + P[i]) == T.charAt(i - 1 - P[i])) { P[i]++; } // 判断是否需要更新 R if (i + P[i] > R) { C = i; R = i + P[i]; } } // 找出 P 的最大值 int maxLen = 0; int centerIndex = 0; for (int i = 1; i < n - 1; i++) { if (P[i] > maxLen) { maxLen = P[i]; centerIndex = i; } } int start = (centerIndex - maxLen) / 2; //最开始讲的求原字符串下标 return s.substring(start, start + maxLen); } ``` 时间复杂度:for 循环里边套了一层 while 循环,难道不是 O ( n² )?不!其实是 O ( n )。不严谨的想一下,因为 while 循环访问 R 右边的数字用来扩展,也就是那些还未求出的节点,然后不断扩展,而期间访问的节点下次就不会再进入 while 了,可以利用对称得到自己的解,所以每个节点访问都是常数次,所以是O ( n )。 空间复杂度:O(n)。 </br> 全文转载自:[知乎:一文让你彻底明白马拉车算法](https://zhuanlan.zhihu.com/p/70532099) 仅做备份留档,以供自己学习使用 最后修改:2023 年 01 月 21 日 © 转载自他站 打赏 赞赏作者 支付宝微信 赞 1 本作品采用 CC BY-NC-SA 4.0 International License 进行许可。